Определение производной функции
Производной функции f(x) в точке x0 называется предел, к которому стремится отношение приращение функции к приращению аргумента, когда приращение аргумента стремится к нулю:
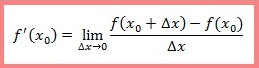
Основные свойства производных

Производная сложной функции
Рассмотрим сложную функцию, аргумент которой также является функцией: h(x)=g(f(x)). Если функция f имеет производную в точке x0, а функция g имеет производную в точке f(x0),то сложная функция h также имеет производную в точке x0, вычисляемую по формуле:
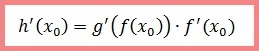
Правило Лопиталя

Достаточные признаки монотонности функции.
Если f '(x)>0 в каждой точке интервала (a,b),то функция f(x) возрастает на этом интервале.
Если f '(x)<0 в каждой точке интервала (a,b), то функция f(x) убывает на этом интервале.
Необходимое условие экстремума.
Если x0 -точка экстремума функции f(x) и производная f ' существует в этой точке, то f '(x0)=0.
Вторая производная.
Если производная f '(x) функции f(x) дифференцируема в точке x0, то её производная называется второй производной функции f(x) в точке x0, и обозначается f ''(x0).