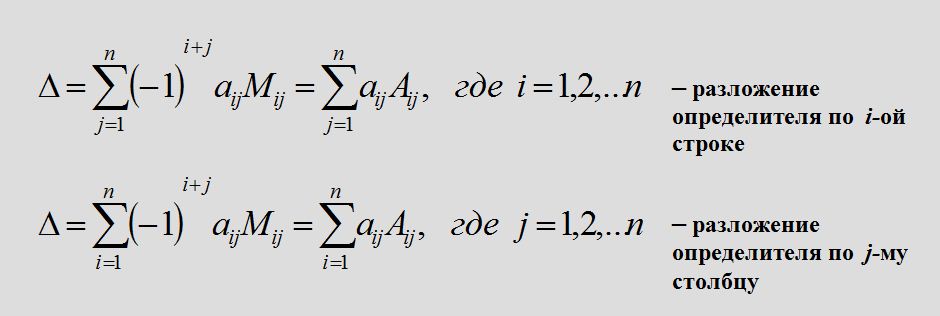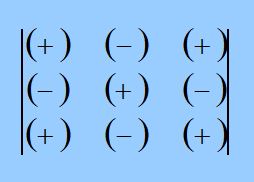2.6. Теорема Лапласа

Миноры и алгебраические дополнения играют важную роль в алгебре и её приложениях. Одним из таких применений является теорема о способе вычисления определителей.

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения: 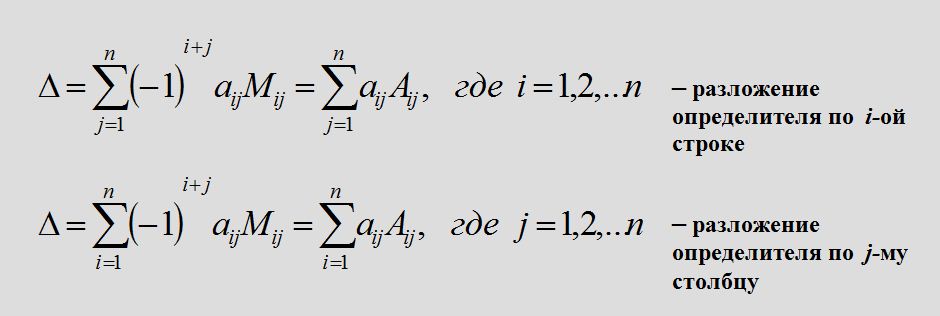Эта формула сводит вычисление определителя n-го порядка к вычислению n определителей (n – 1)-го порядка. Определитель можно вычислять разложением его по элементам различных рядов. Удобно вычислять по элементам того ряда, который содержит элементы, равные нулю.

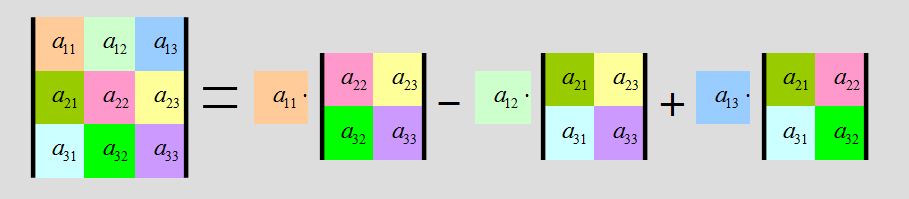
Рассмотрим формулу вычисления определителя третьего порядка разложением его по элементам первой строки.

В силу определения имеем: алгебраическое дополнение равно минору, взятому со своим знаком, если сумма номеров строки и столбца (сумма индексов) число четное, и алгебраическое дополнение элемента a_ij равно минору, взятому с противоположным знаком, если (i+j) есть число нечетное.

Для практического использования удобно представить расположение знаков, с которыми нужно брать миноры в определителе третьего порядка для получения алгебраических дополнений; на схеме (+) – свой знак, (-) – противоположный.

Примеры вычисления определителей третьего порядка с помощью теоремы Лапласа Примеры вычисления определителей четвертого порядка с помощью теоремы Лапласа В результате вычисления определителя разложением его по элементам различных рядов получен один и тот же результат.